译注

• 本文关键词：人工智能，机器学习，神经网络，遗传算法，仿真
• 偶然看到，本文写得非常深入浅出，不像国内很多“科普文”通篇公式和符号，生怕外行看得懂似的，特意整理翻译。翻译不易，转载请在文章开头注明出处：http://www.telihai.com/archives/9319/
• 原文使用 Rust WebAssembly 实现这个程序，但不懂编程也能看懂原理。
• 原文链接：Learning to Fly: Let’s create a simulation in Rust! (pt 1)

正文

在本系列中，我们将使用神经网络和遗传算法创建进化仿真。

我将向您介绍基本神经网络和遗传算法的工作原理，然后我们将在 Rust 中实现它们， 并将我们的应用程序编译到 WebAssembly 中，最终得到：

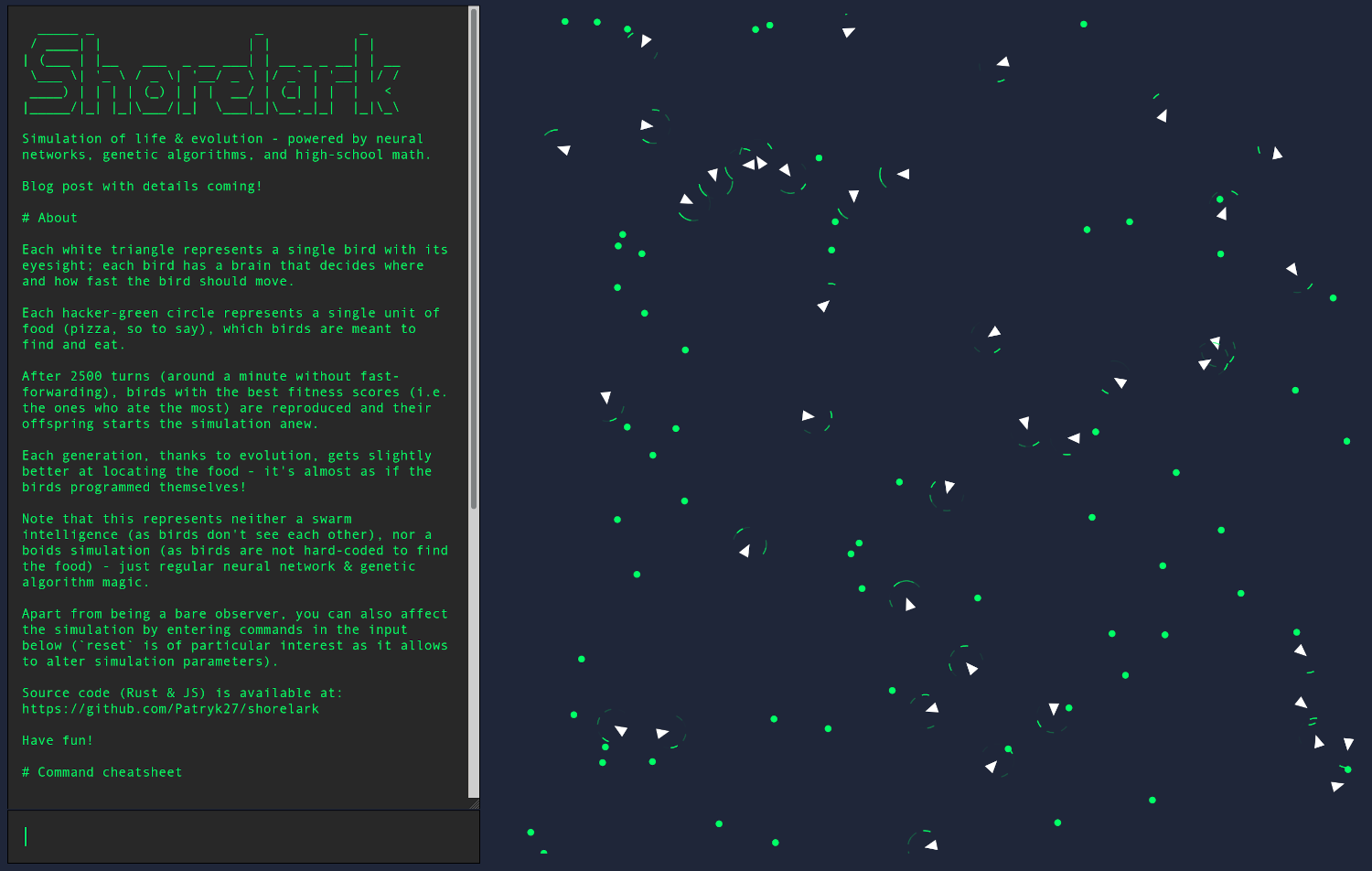
图 1：演示地址

本系列文章将分为几篇文章，大致如下：

1. 领域介绍（我们要模拟什么，神经网络和遗传算法如何工作），
2. 实施神经网络，
3. 实施遗传算法，
4. 实现眼睛，大脑和模拟本身。

事前调查：我会尽力解释所有概念，但是，如果您在任何时候感到迷茫，请随时阅读本文的最后一部分——它包含指向可能有助于理解的资源链接（多数为流行科学）。

好奇吗？让我们开始：设计。

设计

让我们从明确定义目标开始：我们要模拟什么？

总体思路是，我们有一个代表世界的二维平面：

这个世界由鸟类组成（因此项目的原始代号为 Shorelark）：

……和食物（某种抽象的，富含蛋白质和纤维）：

每只鸟都有自己的视野，可以找到食物：

……以及控制鸟类身体（移动速度和旋转角度）的大脑。

我们的魔力在于，与其将我们的鸟硬编码为某种特定的行为（例如“去吃视野内最近的食物”），我们将采用一种更有趣的方法：

大脑

如果您仔细观察，您会发现大脑不过是某些输入到某些输出的函数，例如：

f(视, 嗅, 听, 味, 触) = (速度, 方向)

由于我们的鸟类只有一种感觉输入，因此它们的大脑可以近似为：

f(看) = 移动

从数学上讲，我们可以将该函数的输入（即生物眼）表示为数字列表，每个数字（即生物感光体）描述最近的物体（即食物）有多近：

（0.0 - 视野中没有物体，1.0 - 物体就在前方。）

至于输出，我们将使函数返回一个元组 (Δspeed, Δrotation)（译注：(delta speed：速度差, delta rotation：角度差)）。

例如，大脑告诉我们 (0.1, 45) 的意思是“身体，请以 0.1 单位加速度并 45 度顺时针旋转”，而 (0.0, 0) 的意思是“身体，请保持当前路线”。

最后，让我们谈谈房间里的大象：所以大脑基本上是 f(eyes)，对吧？但是，我们如何找出下面等号后的 what？

神经网络：简介

同为人类，您可能会意识到大脑是由通过突触连接的神经元组成的：

图 2：我试着绘制的神经元；不按比例

突触在神经元之间携带电信号和化学信号，而神经元“决定”给定信号是否应进一步传播或停止。最终，这使人们能够识别字母，吃球芽甘蓝，并在 Twitter 上发表刻薄的言论。

由于其固有的复杂性，生物神经网络并不是最容易模拟的（有人可能会说神经元不是网状的），这使得一些聪明的人发明了一种称为人工神经网络的数学结构，该结构允许用数学近似——不完全是——大脑的行为。

人工神经网络（我将其简称为神经网络）在对数据集进行泛化方面（例如，学习猫的形像）非常突出，因此它们发现了其在面部识别（例如相机），语言翻译（例如 GNMT）中的用途。），以及——在我们的示例中——对彩色像素进行一些评估。（译注：这里的原文是 to steer colorful pixels for a handful of reddit karma. reddit karma 是国外网站 Reddit 的积分系统。）

我们将关注的特定类型的网络被称为 feedforward neural network（前馈神经网络，FFNN）……

……看起来像这样：

图 3：多层感知器（MLP）的示例，也称为FFNN

这是具有五个突触和三个神经元的 FFNN 的布局，它们全部组织为两层：输入层（在左侧）和输出层（在右侧）。

在它们之间也可能存在一些层，在这种情况下，它们被称为隐藏层——它们提高了网络理解输入数据的能力（想想：大脑越大，在某种程度上它就越可能理解“更抽象的”）。

与生物神经网络（背负着电信号）相反，FFNN 的工作原理是在输入端接受一些数字，然后在整个网络中逐层传播（前馈）这些数字；出现在最后一层的数字决定了网络的答案。

例如，如果您“喂给”神经网络一张图片，则可能会收到如下响应：

• 0.0 - 此图片不包含吃烤意面的橘猫，
• 0.5 - 此图片可能包含一只吃烤意面的橘猫，
• 1.0 - 此图片中肯定包含一只吃烤意面的橘猫。

网络也可能返回许多值（输出值的数量等于输出层中神经元的数量）：

• (0.0, 0.5) - 该图片不包含橘猫，但可能包含烤意面，
• (0.5, 0.0) - 此图片可能包含一只橘猫，但不包含烤意面。

输入和输出数字的含义由您决定——在这种情况下，我们只是想像有某种以这种方式运行的神经网络，但实际上是基于您所准备的所谓训练数据集（“给这张图片，应该返回 1.0”，“给那张图片，应该返回 0.0”）。

考虑到 FFNN 的一般概述，现在让我们迈出下一步，了解可实现所有这些功能的魔力。

神经网络：深入

FFNN 依靠两个构件：神经元和突触。

一个神经元（通常是用圆圈表示）接受某些输入值，处理它们，并且返回一些输出值；每个神经元至少有一个输入，最多有一个输出：

图 4：具有三个突触的单个神经元

此外，每个神经元都有偏倚（译注：下文也可能用“偏差”代替）：

图 5：具有三个突触和标注了偏倚值的单个神经元

偏差就像神经元的 if 语句一样——除非输入足够强（高），否则它允许神经元保持不活动状态（返回零输出）。形式上我们可以说偏倚可以调节神经元的激活阈值。

想象一下，您有一个包含三个输入的神经元，每个输入确定它是否看到烤意面（1.0）或否（0.0）——现在，如果您要创建一个神经元，当它看到至少两份烤意面时被激活，您只需创建偏倚 -1.0 的神经元；这样，您的神经元的“自然”状态将处于 -1.0（非活动状态），一份烤意面：0.0（仍处于非活动状态）和两份：1.0（激活状态，不错）。

如果您对我烤意面的隐喻不感兴趣，那么您可能会发现这个面向数学的解释会更有用。

除神经元外，我们还有突触——突触就像一条线，将一个神经元的输出连接到另一个神经元的输入。每个突触都有一定的权重：

图 6：具有三个标注了权重的突触的单个神经元

权重是一个因子（因此，在每个数字前面加一个 x 以强调其乘法性质），因此权重为：

• 0.0 意味着突触实际上已经死亡（它不会将任何信息从一个神经元传递到另一个神经元），

• 0.3 表示如果神经元 A 返回 0.7，则神经元 B 将接收到 0.7 * 0.3 ≈ 0.2，

• 1.0 其突触是有效直通——如果神经元 A 返回 0.7，神经元 B 就接收 0.7 * 1.0 = 0.7。

记住所有这些知识后，让我们回到我们的网络，并使用一些随机数来填充缺失的权重和偏差：

是多么美丽，不是吗？

让我们看看输入 (0.5, 0.8) 它会怎么想：

重申一下，我们对最右边的神经元（这是我们的输出层）的输出值感兴趣——因为它依赖于先前的两个神经元（来自输入层的神经元），因此我们将从它们开始。

让我们首先关注左上神经元——为了计算其输出，我们首先计算所有输入的加权和：

0.5 * 0.2 = 0.1

……然后，我们加上偏差：

0.1 - 0.3 = -0.2

……并通过所谓的激活函数 钳制该值；激活函数将神经元的输出限制在预定义范围内，从而模拟类似 if 的行为。

最简单的激活函数是整流线性单元（ReLU），基本上是 f32::max（译注：f32::max 是一个非常大的正数）：

如您所见，当我们的加权总和小于零时，神经元的输出将为 0.0——这正是我们当前输出所发生的情况：

max(-0.2, 0.0) = 0.0

译注：max(a, b) 表示在 a 和 b 中取较大那个。

好 现在让我们做左下角的：

# 加权和:
0.8 * 1.0 = 0.8

# 偏差:
0.8 + 0.0 = 0.8

# 激活函数:
max(0.8, 0.0) = 0.8

至此，我们完成了输入层：

……将我们引向最后一个神经元：

# 加权和:
(0.0 * 0.6) + (0.8 * 0.5) = 0.4

# 偏差:
0.4 + 0.2 = 0.6

# 激活函数:
max(0.6, 0.0) = 0.6

……以及网络的输出本身：

0.6 * 1.0 = 0.6

不错，对于我们投入的 (0.5, 0.8)，我们的网络做出了 0.6 的回应。

（由于这只是在完全虚构的网络上进行的练习，因此此数字并不代表任何含义-只是一些输出值。）

总体而言，这是最简单的 FFNN 之一——赋予适当的权重，它能够解决XOR问题，但可能缺乏操纵鸟类的计算能力。

更为复杂的 FFNN，例如：

……的工作方式完全相同：您只需从左到右，逐个神经元地计算输出，直到从输出层中挤出所有数字。

（在那个特定的图上，一些突触重叠，但这并不意味着什么：这只是在平面屏幕上表示多维图的不幸。）

此时，您可能会开始怀疑“等等，我们怎么知道我们网络的权重？”，为此，我得到一个简单的答案：

我们将它们随机化！❤️️

如果您习惯于确定性算法（冒泡排序，有人吗？），这可能会给你一个画外音，但它是事物适用于包含多于少量神经元的网络的方式：你手指交叉，随机化初始权重，与您所得到的一起工作。译注：实在翻不好这句怎么用中文说，反正它的意思是给一些随机的初始权重就可以开始运行了，而不是你去设计一个有针对性的算法，原文：

If you’re accustomed to deterministic algorithms (bubble sort, anyone?), this might feel non-diegetic to you, but it’s the way things go for networks containing more than a few neurons: you cross your fingers, randomize the initial weights, and work with what you got.

注意，我说的是初始权重——一些非零权重，您可以在网络上应用某些算法来改进它（因此，本质上讲就是教它）。

FFNN 最流行的“教学”算法之一是反向传播：

您以“输入这个，应返回那个”（“对于抱枕的图片，应返回枕形”）的形式展示网络上的大量示例（成千上万），然后反向传播会慢慢调整您的网络的权重，直到获得正确的答案为止。

如果您有大量带有标签的示例（例如照片或统计数据），那么反向传播是一个很好的工具，这就是为什么它不符合我们最初的假设的原因：

我们不是统计学家，世界是一个残酷的地方，所以我们希望我们的鸟儿自己搞定所有的学习（而不是给定具体的“因为这个，向左”，“因为那个，向右”）。

解决方案？

遗传算法：简介

回顾一下，从数学的角度来看，我们的根本问题是我们有一个由大量参数定义的函数（使用神经网络表示）：

（我没有费心去画所有的权重，但我希望您能明白这一点——有很多。）

如果我们用一个单精度浮点数（译注：计算机可以表示的小数）表示每个参数，那么仅 3 个神经元和 5 个突触的网络可以有许多不同的组合。

(3.402 * 10^38) ^ (3 + 5) ≈ 1.8 * 10^308

（有多少个浮点数）（译注：1.8 * 10^308 表示 1.8 乘以 10 的 308 次方，相比之下，宇宙中所有基本粒子的总和“只有”约 10^80 个。）

……在我们将其全部检查完之前宇宙都已经走到了尽头。我们当然需要变得更聪明！

由于遍历我们的搜索空间以寻找最佳答案是不可能的，因此我们可以专注于查找次优答案列表这个简单得多的任务。

遗传算法：深入

这是野胡萝卜及其驯化形式：

这种驯化的，广为人知的形式并非并非一帆风顺——这是数百年来选择性育种的结果， 其中考虑到某些因素（例如根茎的质地或颜色）。

如果我们可以用神经大脑做类似的事情，那会很棒吗？如果我们只是像这样创造了一群随机的鸟，并有选择地繁殖了那些看起来最杰出的鸟……

嗯......

事实证明，我们并不是第一个偶然发现这个想法的人——已经存在一个被广泛研究的计算机科学分支，称为进化计算，该分支的全部目的是“按照自然的方式”解决问题。

在所有进化算法中，我们将要研究的具体子类称为遗传算法。

从上至下，遗传算法从一个群体开始：

群体是由个体（有时称为代理）建立的：

一个个体（或代理）是对给定的问题的一个单一可能的解决方案，（群体是一些可能的解决方案的一个集合）。

在我们的例子中，每个个体都将建模一个大脑（或整个鸟类，如果您更喜欢以这种方式进行可视化），但是通常这取决于您要解决的问题：

• 如果您想进化一根天线，那么每个个体就是一根天线。
• 比如如果您尝试制定一个查询计划，那么一个个体就是一个查询计划。

一个个体是由基因（统称为基因组）构建而成的：

图 7：用神经网络权重表示的基因组；基因组可能是数字列表，图形或其他能够为问题解决方案建模的东西

一个基因是被遗传算法评估和调整的单一参数。

在我们的例子中，每个基因都只是神经网络的权重，但是代表问题域并不总是那么简单。

例如，如果您要帮助一个旅行商（译注：旅行商问题是指路线规划问题），其根本问题完全不基于神经网络，单个基因可能是确定推销员旅程的坐标元组 (x, y)（因此，一个个体会描述推销员的完整路径）：

图 8：解决旅行商问题的假设方法——每个方框代表推销员可能的建议行程路径

现在，假设我们有五十只鸟的随机种群——我们将它们传递给遗传算法，会发生什么？

与选择性育种类似，遗传算法从评估每个个体（每个可能的解决方案）开始，以查看哪些在当前种群中是最好的。

从生物学上讲，这等同于漫步到您的花园并检查哪种胡萝卜最鲜艳和最好吃。

评估情况使用所谓的适应度函数返回一个健康分数量化一个特定的个体有多好（这样一个特定的解决方案）是：

图 9：一个适应度函数的示例，该函数根据胡萝卜的根茎的颜色和半径对其进行量化

当涉及遗传算法时，创建可用的适应度函数是最艰巨的任务之一，因为通常有许多度量标准可以用来衡量一个个体。

（即使我们想象的胡萝卜也至少具有三个指标：根茎的颜色，半径和味道，必须将其压缩为一个数字。）

幸运的是，对鸟类而言，我们无需太多选择：我们只定义一只鸟的优劣和它一生所吃的食物量成正比。

吃 30 个食物的鸟比只吃 20 个食物的鸟好，就这么简单。

现在，遗传算法精益求精的时机已经成熟：再现！

从广义上讲，繁殖是指从当前个体开始建立新的（希望有所改善）个体的过程。

这在数学上等同于选择最美味的胡萝卜并种植其种子。

具体发生的是遗传算法随机选择了两个个体（优先选择适应度较高的个体），并使用它们来产生两个新个体（所谓的后代）：

后代是通过获取父母双方的基因组并对其进行交叉（crossover）和突变（mutation）而产生的：

这两个新产生的个体都被推入一个 新种群 池中并重新开始这个过程直到建立了全新的种群为止。然后，当前的种群将被丢弃，整个模拟将从这个新的（希望有所改善！）种群开始。

如您所见，在此过程中存在很多随机性：我们从随机种群开始，我们随机化基因的分布……所以……

代码

让我们以一个悬念结束这篇文章：

$ mkdir shorelark

你能猜出为什么我不使用 cargo new 吗？

在第二部分中，我们将实现一个可行的，粗浅的前馈神经网络——到时见！

资源

在学习本文介绍的主题时，以下是一些我个人认为有用的资源：

神经网络：

• YouTube, 3Blue1Brown - But what is a Neural Network?
• YouTube, Vsauce - The Stilwell Brain

遗传算法：

• YouTube, Jeremy Fisher - Genetic Algorithms
• obitko.com - Genetic Algorithms Tutorial
• Darrell Whitley - A Genetic Algorithm Tutorial

待续

翻译太累了，我得缓缓，最好有人接力翻译。